Introducing the Instruction Set Part 4
This short tutorial examines the shift and rotate instructions. These are useful instructions, but somewhat more specialized than the rest of the instruction set. If you haven't read Part 1, Part 2 or Part 3 yet, you might consider doing so first.
Contents
Shift and Rotate Instructions
The CP1610 offers a rich variety of shift and rotate instructions. Each can shift by one or two positions. The shift instructions only operate on R0 through R3. You cannot use them with R4 through R7.
Click on a given mnemonic to see how it operates.
| SLL Rx[, 2] | Shift Logical Left |
|---|---|
| SLR Rx[, 2] | Shift Logical Right |
| SAR Rx[, 2] | Shift Arithmetic Right |
| SWAP Rx[, 2] | Swap bytes |
| SLLC Rx[, 2] | SLL into Carry |
| SARC Rx[, 2] | SAR into Carry |
| RLC Rx[, 2] | Rotate Left thru Carry |
| RRC Rx[, 2] | Rotate Right thru Carry |
Shifts and rotates are useful for bit manipulation and certain types of mathematics, such as random number generation. Logical shifts (SLL, SLR, SLLC) fill the newly-opened positions with zeros. Arithmetic shifts (SAR, SARC) fill the newly opened positions with copies of bit 15. Logical right shifts can be thought of as "unsigned divide by 2", whereas arithmetic right shifts can be thought of as "signed divide by 2, rounding toward negative."
Shifts can also align numbers with fields packed in a word, or help extract a field in a packed word. For example, the STIC display words in the BACKTAB store the card # to display in bits 2 - 10. To extract a card number, you need to shift right by 3. To insert a card number into a display word, you need to shift left by 3.
Rotates are like shifts, except that they fill the vacated bits with bits from a status register. By itself, this property has no particular mathematical meaning. When rotates combine with shifts, though, they can perform extended-precision operations.
Shift and Rotate Diagram Summary
The following diagrams illustrate the behavior of each of the 8 shift and rotate instructions. Click on the links below for more detail.
| Shifts that do not use Carry and Overflow | Shifts and rotates that do use Carry and Overflow |
|---|---|
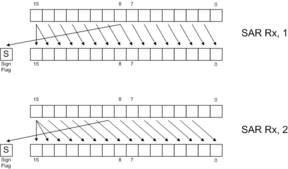 SAR | 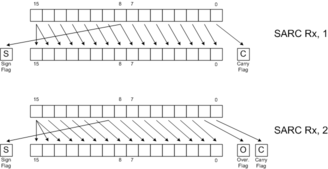 SARC |
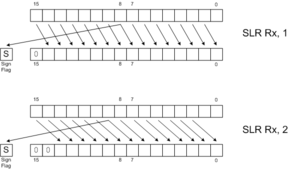 SLR | 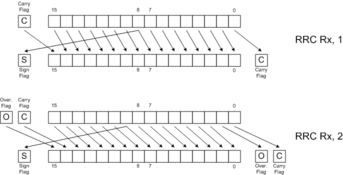 RRC |
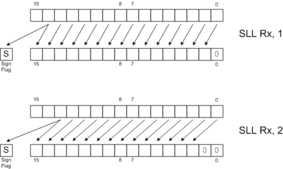 SLL | 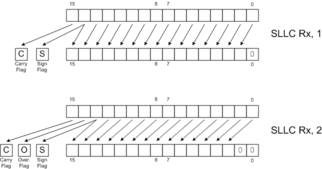 SLLC |
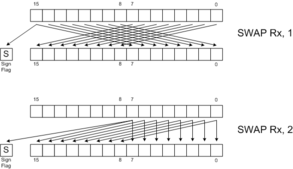 SWAP | 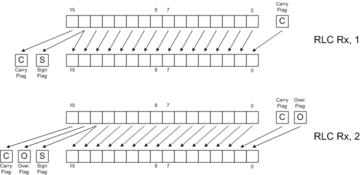 RLC |
Caveats: Non-interruptibility
Shift instructions are Non-interruptible Instructions. Be sure to include an interruptible instruction in a long sequence of shifts or other non-interruptible instructions, otherwise you could cause display glitches.
A useful rule of thumb is to insert an interruptible instruction between every 4 or so non-interruptible instructions. If you can't find an interruptible instruction to move into place, you can use a NOP instruction.
Using Shifts for Multiplication
Shifting values left multiplies them by powers of two. Each bit position shifted corresponds to another power of two. Shifting left one position multiplies by 2; shifting by two positions multiplies by 4. The following table illustrates the relationship between positions shifted and the power of two. The table stops at 8 for brevity's sake.
|
|
You can combine shift and add instructions to perform simple multiplications by constants that aren't powers of two. The following example shows how to multiply the value in R0 by 20, using R1 as a temporary variable.
SLL R0, 2 ; Multiply R0 by 4
MOVR R0, R1 ; Save a copy of original value * 4
SLL R0, 2 ; Multiply R0 by 4 again (original value * 16)
ADDR R1, R0 ; Add (value * 4) to (value * 16), giving (value * 20)
This works by recognizing that "20" is the sum of two powers of two, "4" and "16". In general, you can multiply by any constant by breaking the constant down into its constituent powers of two.
In some cases, it may be more efficient to use subtracts instead of adds. For example, consider the following example that multiplies R0 by 15, using R1 as a temporary register.
MOVR R0, R1 ; Save a copy of original value
SLL R0, 2 ; multiply R0 by 4: R0 = value * 4
SLL R0, 2 ; multiply R0 by 4 again: R0 = value * 16
SUBR R1, R0 ; Subtract original value from result: R0 = value * 15
Using Shifts for Division by Powers of Two
Right shifts divide by powers of two, by default truncating the fractional portion. This is the same as rounding towards negative. With a minor tweak, the same code can round upwards. The following table shows example code sequences for various power-of-two divides on signed numbers and unsigned numbers.
| Number of positions shifted right | Power of 2 divided by | Example Code Sequence for signed, rounding to negative | Example Code Sequence for signed, rounding to positive | Example Code Sequence for unsigned, rounding toward 0 | Example Code Sequence for unsigned, rounding to positive |
|---|---|---|---|---|---|
| 1 | 2 | |
|
|
|
| 2 | 4 | |
|
|
|
| 3 | 8 | |
|
|
|
| 4 | 16 | |
|
|
|
| 5 | 32 | |
|
|
|
| 6 | 64 | |
|
|
|
| 7 | 128 | |
|
|
|
| 8 | 256 | |
|
|
|
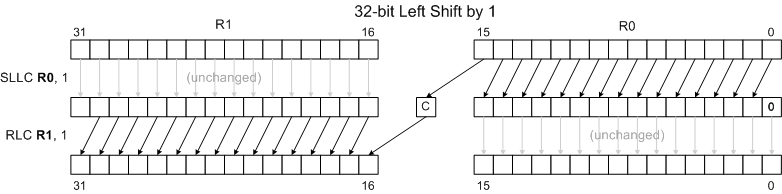
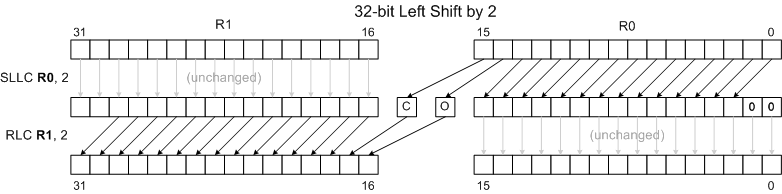
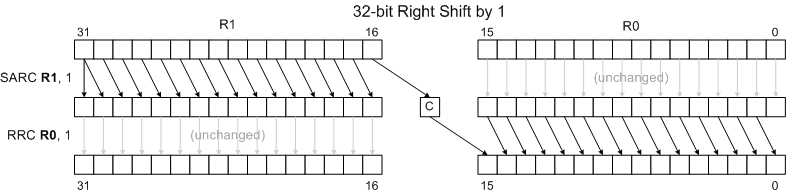
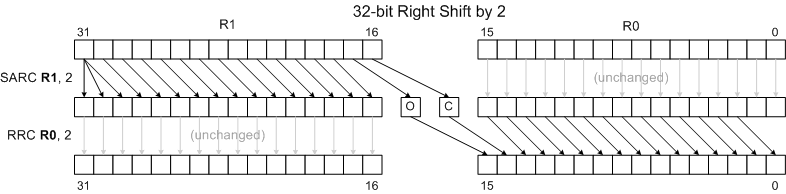
Combining Shifts and Rotates for Extended-Precision Shifts
Rotate instructions combined with shift instructions make it easy to shift values longer than 16 bits. The following examples show how to shift the 32 bit number held in R1:R0 left and right by 1 and 2 positions. (R1 holds bits 16..31 of the 32-bit number.) Note that the diagrams omit the final results of the Carry Flag, Overflow Flag and Sign Flag for clarity and brevity. The rotate instructions do move the shifted-away bits to the C and O flags, though, allowing one to extend the shift to even wider words. See the RLC and RRC pages for more details.
32-bit Left Shift by 1
|
32-bit Left Shift by 2
|
32-bit Right Shift by 1
|
32-bit Right Shift by 2
|
Wrapping Up
At this point, you may wish to revisit the earlier parts of this tutorial:
- Introducing the Instruction Set Part 1: The CPU, Memory and Registers; Primary Instructions and Addressing Modes
- Introducing the Instruction Set Part 2: Single Register and Implied Operand Instructions
- Introducing the Instruction Set Part 3: Branches, Conditional Branches and Calls
Or, you can return to the Programming Tutorials index.